Phương trình toán học là công cụ quan trọng giúp giải quyết các bài toán liên quan đến phương trình hoặc hệ phương trình. Dưới đây là điều kiện phương trình có 2 nghiệm trái dấu và bài tập áp dụng.
Mục Lục
Điều kiện phương trình có 2 nghiệm trái dấu
Một phương trình là một phát biểu mà nói rằng hai biểu thức bằng nhau. Chúng ta có thể tìm ra các giá trị mà thỏa mãn phương trình đã cho thông qua việc áp dụng các phương pháp và quy tắc của toán học.
Dưới đây là những kiến thức cần nhớ khi làm dạng bài tìm m để phương trình có hai nghiệm trái dấu.

Điều kiện phương trình có 2 nghiệm trái dấu
Xem ngay: hệ phương trình có nghiệm duy nhất khi nào để biết thêm thông tin
Định lý vi-ét
Nếu phương trình: ax2 + bx + c = 0 (a khác 0) có hai nghiệm x1; x2 phân biệt thì:
S = x1 + x2 = – b/a
P = x1x2 = c/a
+ Lưu ý: Trước khi áp dụng định lý Vi ét, ta cần tìm điều kiện để phương trình có 2 nghiệm phân biệt.
Xác định dấu các nghiệm của phương trình bậc hai:
Điều kiện để phương trình có hai nghiệm trái dấu, cùng dấu, cùng dương, cùng âm,…
+ Để phương trình có hai nghiệm phân biệt trái dấu thì P < 0
+ Để phương trình có hai nghiệm phân biệt cùng dấu thì: >0, P > 0
+ Để phương trình có hai nghiệm phân biệt cùng dấu dương thì: > 0, P > 0, S > 0.
+ Để phương trình có hai nghiệm phân biệt cùng dấu âm thì > 0, P > 0, S < 0
Tính m để phương trình bậc hai có hai nghiệm trái dấu nhanh nhất
Bài 1: Tìm m để phương trình x2 – (m2 + 1)x +m2 – 7m + 12 = 0 có 2 nghiệm trái dấu
Gợi ý đáp án
Để phương trình có hai nghiệm phân biệt trái dấu thì P < 0.
Để phương trình có hai nghiệm phân biệt trái dấu thì P < 0
- m2 – 7m + 12 < 0
- (m – 3)(m – 4) < 0
Xảy ra hai trường hợp:
Trường hợp 1: 3 < m < 4
Trường hợp 2: m < 3, m > 4 (vô lý)
Bài 2: Tìm m để phương trình x2 – (2m + 3)x + m = 0 có hai nghiệm phân biệt cùng dấu âm
Bài 3: Tìm m để phương trình 3{x^2} – 4mx + {m^2} – 2m – 3 = 0 có hai nghiệm phân biệt cùng dấu.
Bài 4: Tìm m để phương trình {x^2} – 2mx + 2m – 4 = 0 có hai nghiệm phân biệt cùng dấu dương. Hướng dẫn: Để phương trình có hai nghiệm cùng dấu dương
Bài tập tìm m để phương trình có 2 nghiệm trái dấu
Bài 1: Tìm m để phương trình {x^2} – 8x + m + 5 = 0 có hai nghiệm phân biệt:
Bài 2: Tìm m để phương trình {x^2} – 2mx + 5m – 4 = 0 có hai nghiệm phân biệt:
Bài 3: Tìm m để phương trình 2{x^2} + (2m -1)x + m – 1 = 0 có hai nghiệm phân biệt cùng dấu âm
Bài 4: Tìm m để phương trình {x^2} – 2mx – 6m – 9 = 0 có hai nghiệm phân biệt trái dấu thỏa mãn x_1^2 + x_2^2 = 13
Bài 5: Tìm m để phương trình {x^2} – 2(m +1)x + m + 4 = 0 có hai nghiệm phân biệt cùng dấu dương
Bài 6: Tìm m để phương trình {x^2} – 2(m+1)x + m + 4 = 0 có hai nghiệm phân biệt:
a) Trái dấu. b) Cùng dấu. c) Cùng dấu âm. d) Cùng dấu dương.
Bài 7: Tìm m để phương trình {x^2} – (2m+3)x + m = 0 có hai nghiệm phân biệt:
a) Trái dấu. b) Cùng dấu. c) Cùng dấu âm. d) Cùng dấu dương.
Bài 8: Tìm m để phương trình {x^2} – (m+1)x + m = 0 có hai nghiệm phân biệt cùng dấu dương
Bài 9: Cho phương trình {x^2} + (m + 2)x + m = 0. Tìm m để phương trình có hai nghiệm phân biệt cùng dấu. Khi đó hai nghiệm mang dấu gì?
Bài 10: Tìm m để phương trình {x^2} – 2mx + 2m – 4 = 0 có hai nghiệm phân biệt cùng dấu âm
Bài 11: Cho phương trình x2 – (2m + 1)x + m2 + m – 6 = 0. Tìm m để phương trình có 2 nghiệm âm. Lựa chọn một trong những đáp án sau:
- m > 2
- m < -4
- m > 6
- m < -3
Bài 12: Cho phương trình: x2 – 2mx + 2m – 4 = 0. Có bao nhiêu giá trị nguyên của m nhỏ hơn 2020 để phương trình có 2 nghiệm dương phân biệt.
A.2016 B. 2017 C. 2018 D. 2019
Bài 13: Cho phương trình: x2 – 8x + m + 5 = 0. Gọi S là tập hợp chứa tất cả các giá trị nguyên của m để phương trình có 2 nghiệm cùng dấu. Tính tổng tất cả các phần tử của S
A.30 B. 56 C. 18 D. 29
Bài 14: Cho phương trình mx2 + 2(m – 2)x + m – 3 = 0. Xác định m để phương trình có hai nghiệm trái dấu.
A.m > 0 B. 1 < m < -1 C. 0 <m < 3 D. m < 3
Bài 15: Tìm giá trị m để phương trình 2×2 + mx + m – 3 = 0 có 2 nghiệm trái dấu và nghiệm âm có giá trị tuyệt đối lớn hơn nghiệm dương. A. 0 < m < 3 B. -1 < m < 3 C. m < 2 D. m > -3
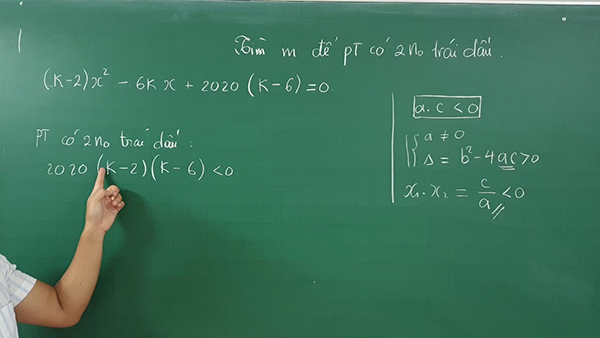
Bài tập vận dụng
Click ngay: điều kiện để phương trình bậc 3 có 3 nghiệm để biết thêm thông tin
Bài 16: Tìm các giá trị của m để các phương trình dưới đây có nghiệm
1, {x^2} + 2(m – 3)x + {m^2} – 3 = 0
2, {x^2} – 2(m +2)x + {m^2} + 4m + 3 = 0
3, {x^2} – 2(m + 6)x + m + 1 = 0
4, {x^2} – 2mx + {m^2} – m + 1 = 0
5, 3{x^2} – 2x – m + 1 = 0
6, {x^2} – 2x + m – 1 = 0
7, {x^2} – 2mx + m – 2 = 0
8, {x^2} – 5x + m = 0
9, {x^2} – 2mx + {m^2} – 1 = 0
10, {x^2} – 4x + m + 2 = 0
11, {x^2} + 2(m+ 5)x + {m^2} – 3 = 0
12, {x^2} – 2(m-1)x + {m^2} – 3m = 0
13, {x^2} + 2mx + {m^2} + m – 3 = 0
Như vậy qua bài viết trên chúng ta đã biết được điều kiện phương trình có 2 nghiệm trái dấu và bài tập áp dụng. Chúc các em thành công!